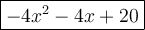Question

Help my with this problem please 50 points

Answer 1

`-4x^2-4x+20`

Explanation:

Since we're subtracting the entire quadratic, we can place the second equation in parentheses and distribute the subtraction sign.

`2x^2-9x+8-(6x^2-5x-12)\\2x^2-9x+8-6x^2+5x+12\\2x^2-6x^2-9x+5x+8+12\\-4x^2-4x+20`

Answer 2

`-4x^2-4x+20`

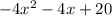
Explanation:

To find the difference of the two quadratic expressions, subtract the second expression from the first expression:

`\implies (2x^2-9x+8)-(6x^2-5x-12)`

Remove the parentheses and apply the distributive law

`-\left(a-b\right)=-a+b`

`\implies 2x^2-9x+8-6x^2+5x+12`

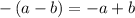
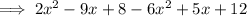
Collect like terms:

`\implies 2x^2-6x^2+5x-9x+8+12`

Combine like terms:

`\implies -4x^2-4x+20`

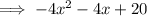
Therefore, the difference of the two quadratic expressions is:

`\large \boxed{-4x^2-4x+20}`