Question

Divide 2/3 by 8/15. Simplify your answer

Answer 1

The correct answer is: "
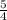`(5)/(4)` " ; {written as an improper fraction} ;

or: " 1.25 " ; {written as a decimal value} ;
or: "
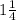`1(1)/(4)` " ; {written as a mixed number fraction}.
__________________

Explanation:

Given:
`(2)/(3)` ÷
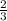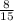`(8)/(15)` = ? {for which we shall solve}.

Note: 'Dividing by' a value; results in the same value as 'multiplying by' its reciprocal value [that is: 'multiplying by its inverted form'].

This is especially noteworthy in problems that involve 'dividing by fractions'.

So, to solve and simply our given problem:

`(2)/(3) * (15)/(8)` = ? ;
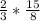Note: The 2 cancels out to 1 ; and the 8 cancels out to 4 ;
The 3 cancels out to 1 ; and the 15 cancels out to 5 ;
→ since: {8 ÷ 4 = 2 } ; & {2 ÷ 2 = 1} ;
and :

→ since: {15 ÷ 3 = 5 } ; & {3 ÷ 3 = 1 } .
______
We can rewrite our "further simplified" expression as:
→
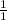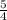`(1)/(1)` *
`(5)/(4)` ;

= " 1 *
`(5)/(4)` " ;

= "
`(5)/(4)` " .

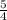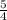Further explanations:
1) Note: Re: the "commutative property" of multiplication:
" a * b = b * a " ; or, write as: " ab = ba " ;
As such: " 1 * \frac{5}{4} " ; is the same as:
↔ "
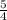`(5)/(4)` * 1 " .

2) Note: Re: the identity property of multiplication:
Any value, multiplied by "1", results in/ retains its same value}.
As such; our calculated value:
"
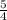`(5)/(4)` * 1 " = \frac{5}{4} " .

3) Note: Re: the division of one (1) property of division:
Any value, divided by "1" ; results in that same initial value.
As such: our calculated value: "
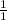`(1)/(1)` = (1 ÷ 1) = 1 " ;

4) Note: Re: the division by itself property of division:
Any value (except "0"), divided by itself, is equal to "1 " ;
As such: our calculated value: "
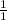`(1)/(1)` = (1 ÷ 1) = 1 " ;
______

So, this answer—which is the most simplified, improper fraction—
is: "
`(5)/(4)` " .

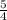Or, to write as a mixed fraction:
Use the mnemonic:

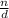`(n)/(d)` = M
`(a)/(d)` ;

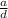That is: "numerator/denominator = M(
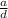`(a)/(d)` )" ; {"M a/d" !} l

⇒ in which M is the [calculated singular whole number portion within the mixed number equivalent] ;
⇒ followed by "
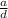`(a)/(d)` " ; in which d is the same denominator as that of the improper fraction ;
⇒ & in which a is the calculated numerator value for the fraction portion for this number ;

So: " \frac{5}{4}} " = (5 ÷ 4) = 1.25 = 1
`(1)/(4)` " .
______

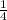Long division method:
__________________________________________
1 R 1 ; ⇒ 1 + (1/4) ; that is; " 1 + (remainder) / (divisor)";
4⟌5 → 1 + ( 1 / 4) ;
− 4 = " 1
`(1)/(4)` ".
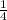1 ; So, "
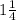`1(1)/(4)` " ; as a mixed number fraction.

or: Use a fraction calculator to convert improper fractions into mixed number fractions.

________________________
or: Use a calculator: " {5 ÷ 4} = 1.25 " .

____
The correct answer is: "
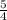`(5)/(4)` " ; {written as an improper fraction} ;

or: " 1.25 " ; {written as a decimal value} ;
or: "
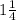`1(1)/(4)` " ; {written as a mixed number fraction}.
____

Hope this answer is helpful!

Wishing you the best!

____

Answer 2

5/4

Explanation:

(2/3)/(8/15)

= (2/3)(15/8)

= (2*15)/(3*8)

= 30/24

= 5/4