Question

You receive an allowance on the first of every month starting on January 1st. Each month, your allowance increases by $2.50. When you sum up all the allowance you received that year in December, it totals $225. Model the amount of allowance you received each month.

Equation?
Continuous or Discrete?

Answer 1

Equation is
`a_n = 2.50n + 2.50`

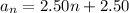
This is discrete

=======================================================

Step-by-step explanation:

There are n = 12 months in a year.

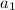`a_1` = first term = x

d = common difference = 2.50, which is the amount the allowance is increasing month to month.

`S_n = \text{Sum of the first n terms of an arithmetic sequence}\\\\S_n = (n/2)*(2a_1 + d(n-1))\\\\S_(12) = (12/2)*(2\text{x} + 2.50(12-1))\\\\S_(12) = 6(2\text{x} + 27.5)\\\\S_(12) = 12\text{x} + 165\\\\`

The sum of the first n = 12 terms of the arithmetic sequence is 12x+165, where x is the first term (i.e. the allowance on January 1st).

We're told that this total is $225. We'll set the value of
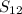`S_(12)` equal to 225 and solve for x.

`S_(12) = 225\\\\12\text{x} + 165 = 225\\\\12\text{x} = 225 - 165\\\\12\text{x} = 60\\\\\text{x} = 60/12\\\\\text{x} = 5`

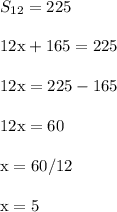
Therefore, you got $5 on January 1st. Then 5+2.50 = 7.50 dollars on February 1st. Then 7.50+2.50 = 10 dollars on March 1st. And so on, until reaching December. All of those dollar amounts then should add to $225 to help confirm the answer.

This equation is discrete because the terms are finite from n = 1 to n = 12. We can't have a midpoint of say between months 3 and 4. It doesn't make sense to have month 3.5 for instance. There's only a set amount of payments.

--------

Now that we know
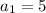`a_1 = 5` is the first term, we can then determine the value of any allowance value for any given value of n.

`a_n = \text{nth term of arithmetic sequence}\\\\a_n = a_1 + d(n-1)\\\\a_n = 5 + 2.50(n-1)\\\\a_n = 5 + 2.50n-2.50\\\\a_n = 2.50n + 2.50\\\\`

Let's see what the allowance would be for month n = 2

`a_n = 2.50n + 2.50\\\\a_(2) = 2.50(2) + 2.50\\\\a_(2) = 5 + 2.50\\\\a_(2) = 7.50\\\\`

The allowance for month n = 2 (aka February) is $7.50, which was mentioned earlier in the previous section. I'll let you confirm the other values of n.

Keep in mind that n is a positive whole number in the set {1,2,3,...,10,11,12}. It might help to make a table of values.