Question

Please help me solve this problem ASAP

Answer 1

`\bold{\huge{\blue{\underline{ Solution }}}}`

Given :-

• The right angled below is formed by 3 squares A, B and C
• The area of square B has an area of 144 inches ²
• The area of square C has an of 169 inches ²

To Find :-

• We have to find the area of square A?

Let's Begin :-

The right angled triangle is formed by 3 squares

We have,

• Area of square B is 144 inches²
• Area of square C is 169 inches²

We know that,

`\bold{ Area \: of \: square = Side × Side }`

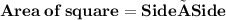
Let the side of square B be x

Subsitute the required values,

`\sf{ 144 = x × x }`

`\sf{ 144 = x² }`

`\sf{ x = √144}`

`\bold{\red{ x = 12\: inches }}`

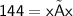
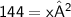
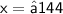
Thus, The dimension of square B is 12 inches

Now,

Area of square C = 169 inches

Let the side of square C be y

Subsitute the required values,

`\sf{ 169 = y × y }`

`\sf{ 169 = y² }`

`\sf{ y = √169}`

`\bold{\green{ y = 13\: inches }}`

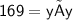
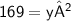
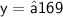
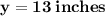
Thus, The dimension of square C is 13 inches.

Now,

It is mentioned in the question that, the right angled triangle is formed by 3 squares

The dimensions of square be is x and y

Let the dimensions of square A be z

Therefore, By using Pythagoras theorem,

• The sum of squares of base and perpendicular height equal to the square of hypotenuse

That is,

`\bold{\pink{ (Perpendicular)² + (Base)² = (Hypotenuse)² }}`

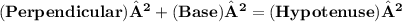
Here,

• Base = x = 12 inches
• Perpendicular = z
• Hypotenuse = y = 13 inches

Subsitute the required values,

`\sf{ (z)² + (x)² = (y)² }`

`\sf{ (z)² + (12)² = (169)² }`

`\sf{ (z)² + 144 = 169}`

`\sf{ (z)² = 169 - 144 }`

`\sf{ (z)² = 25}`

`\bold{\blue{ z = 5 }}`

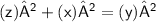
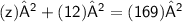
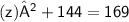
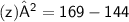
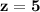
Thus, The dimensions of square A is 5 inches

Therefore,

Area of square

`\sf{ = Side × Side }`

`\sf{ = 5 × 5 }`

`\bold{\orange{ = 25\: inches }}`

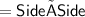
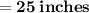
Hence, The area of square A is 25 inches.