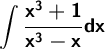
We rewrite the integrand.
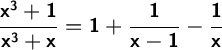
We integrate terms by terms:
The integral of the constants have this constant multiplied by the variable of integration.
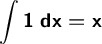
That u = x -1. Then that du = dx and we put du.
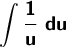
Integral 1/u is log(u). If you now substitute u further into:
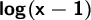
The integral of the product of a function by a constant is the constant times the integral of this function:
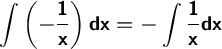
Integral 1/u is log(x). Therefore, the result is: -log(x).
The result is: x - log(x) + log(x - 1)