Question

The coordinates of ∆ABC are A(-3, 2), B(5, 8) & C(11, 0). Which type of triangle is ∆ABC? Select All that apply.

Answer 1

Given:

The coordinates of ∆ABC are A(-3, 2), B(5, 8) & C(11, 0).

To find:

The type of the given triangle.

Solution:

Distance formula:

`D=√((x_2-x_1)^2+(y_2-y_1)^2)`

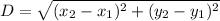
Using the distance formula, we get

`AB=√((5-(-3))^2+(8-2)^2)`

`AB=√((8)^2+(6)^2)`

`AB=√(64+36)`

`AB=√(100)`

`AB=10`

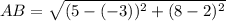
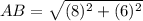
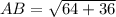
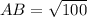
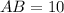
Similarly,

`BC=√((11-5)^2+(0-8)^2)`

`BC=√((6)^2+(8)^2)`

`BC=√(36+64)`

`BC=√(100)`

`BC=10`

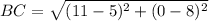
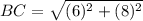
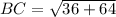
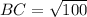
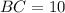
And,

`AC=√((11-(-3))^2+(0-2)^2)`

`AC=√((14)^2+(-2)^2)`

`AC=√(196+4)`

`AC=√(200)`

`AC=10√(2)`

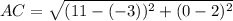
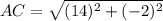
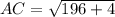
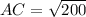
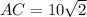
Two sides of the triangle are equal, i.e.,
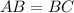`AB=BC`. So, the triangle is an isosceles triangle.

Sum of square of two smaller side is

`AB^2+BC^2=10^2+10^2`

`AB^2+BC^2=100+100`

`AB^2+BC^2=200`

`AB^2+BC^2=AC^2`

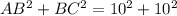
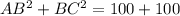
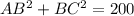
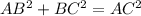
Using the Pythagoras theorem, we can say that the given triangle is a right triangle.

Therefore, the correct options are B and F.