Given:
The coordinates of ∆ABC are A(-3, 2), B(5, 8) & C(11, 0).
To find:
The type of the given triangle.
Solution:
Distance formula:
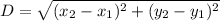
Using the distance formula, we get
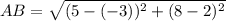
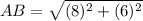
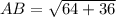
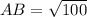
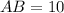
Similarly,

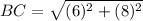

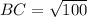
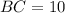
And,
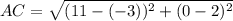
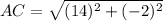
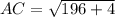
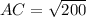
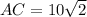
Two sides of the triangle are equal, i.e.,
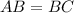 . So, the triangle is an isosceles triangle.
. So, the triangle is an isosceles triangle.
Sum of square of two smaller side is
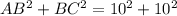
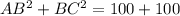
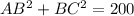
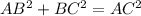
Using the Pythagoras theorem, we can say that the given triangle is a right triangle.
Therefore, the correct options are B and F.