Given:
The four table of values.
To find:
The table whose linear function has slope 2.
Solution:
Slope formula:
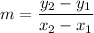
Consider any two points from each table and find the slope for each table.
For table 1, the two points are (2,1) and (6,-1). So, the slope of the linear function is:
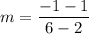
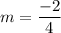
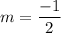
For table 2, the two points are (0,8) and (2,4). So, the slope of the linear function is:
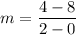
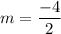
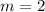
For table 3, the two points are (-4,4) and (-2,5). So, the slope of the linear function is:
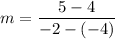
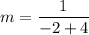
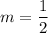
For table 4, the two points are (-2,0) and (0,4). So, the slope of the linear function is:
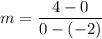
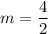
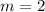
Table 4 is the only table that represents a linear function whose slope is 2.
Therefore, the correct option is 4, Table 4.