Answer:
The two points used to find the slope:
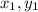 : 2,30
: 2,30
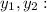 4,10
4,10
Final equation: y = -10x + 50
Explanation:
From a fellow 8th grader <3
First, let's review the slope of a line: y = mx + b
Where m is the slope, and b the y-intercept
Let's find the slope. To do this I will select 2 points from this graph, and using the slope formula I will calculate it
Slope formula:
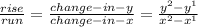
To get the most accurate answer, I will be using the 2 points given that are directly on the line:
1 = (2, 30)
2 = (4, 10)
Slope:
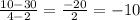
m = -10
It makes sense that it is a negative, since the graph continues downwards.
Let's update our equation: y = -10x + b
We can see that the line intersects the y-axis at y = 50
Plug this into our b-value:
y = -10x + 50
Now, I would recommend using a graphing calculator (like a TI-83) or an online one (like desmos) to double check this. I have attached a screenshot of this line on desmos. From there we can see if this line matches up with the one seen on your graph.
Our answer is:
The two points used to find the slope:
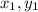 : 2,30
: 2,30
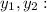 4,10
4,10
Final equation: y = -10x + 50
Please let me know if this helped you, and if this was the correct answer! If it is incorrect I will do my best to revise my answer.