Question

A sample of gas has a volume of 2.50 L at 536 kPa and 75.0 °C. What is the pressure (in atm) of the gas if it expands to 3.75 L at 25.0 °C?

How do i start this?

Answer 1

3.02 atm

Step-by-step explanation:

To find the final pressure, you need to use the Combined Gas Law:

`(P_1V_1)/(T_1)=(P_2V_2)/(T_2)`

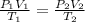
In this equation, "P₁", "V₁", and "T₁" represent the initial pressure, volume, and temperature. "P₂", "V₂", and "T₂" represent the final pressure, volume, and temperature. You first need to convert the temperatures from Celsius to Kelvin (1°C = 273 K). You should convert the initial pressure from kPa to atm (1 atm = 101.3 kPa).

P₁ = 536 kPa / 101.3kPa = 5.29 atm P₂ = ? atm

V₁ = 2.50 L V₂ = 3.75 L

T₁ = 75.0 °C + 273 = 348 K T₂ = 25.0°C + 273 = 298 K

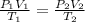`(P_1V_1)/(T_1)=(P_2V_2)/(T_2)` <----- Combined Gas Law

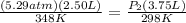`((5.29atm)(2.50L))/(348K)=(P_2(3.75L))/(298K)` <----- Insert values

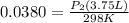`0.0380=(P_2(3.75L))/(298K)` <----- Simplify left side

`11.32 = P_2(3.75L)` <----- Multiply both sides by 298 K

`3.02 = P_2` <----- Divide both sides by 3.75 L