Question

NO LINKS! Please help me with this problem #4l​

Answer 1

`((x-1)^2)/(64)-((y-4)^2)/(80)=1`

• Center = (1, 4)
• Vertices = (-7, 4) and (9, 4)
• Foci = (-11, 4) and (13, 4)

Explanation:

Standard equation of a horizontal hyperbola (opening left and right):

`\boxed{((x-h)^2)/(a^2)-((y-k)^2)/(b^2)=1}`

where:

• Center = (h, k)
• Vertices = (h±a, k)
• Co-vertices = (h, k±b)
• Foci = (h±c, k) where c² = a² + b²

Given:

• Center = (1, 4)
• Vertices = (-7, 4) and (9, 4)
• Point on the hyperbola = (-11, -6)

Therefore:

• h = 1
• k = 4

Find the value of a using the x-values of the vertices:

`\begin{aligned}\implies h-a &= -7\\1-a &= -7\\a &= 8\end{aligned}`

`\begin{aligned}\implies h+a &= 9\\1+a &= 9\\a &= 8\end{aligned}`

Therefore, a = 8.

Substitute the values of h, k and a into the formula:

`\implies ((x-1)^2)/(8^2)-((y-4)^2)/(b^2)=1`

`\implies ((x-1)^2)/(64)-((y-4)^2)/(b^2)=1`

Substitute the given point on the hyperbola (-11, -6) into the equation and solve for b²:

`\implies ((-11-1)^2)/(64)-((-6-4)^2)/(b^2)=1`

`\implies ((-12)^2)/(64)-((-10)^2)/(b^2)=1`

`\implies (144)/(64)-(100)/(b^2)=1`

`\implies (144)/(64)-1=(100)/(b^2)`

`\implies (144)/(64)-(64)/(64)=(100)/(b^2)`

`\implies (80)/(64)=(100)/(b^2)`

`\implies (5)/(4)=(100)/(b^2)`

`\implies b^2=(4 \cdot 100)/(5)`

`\implies b^2=(400)/(5)`

`\implies b^2=80`

Therefore, the equation of the hyperbola is:

`\boxed{((x-1)^2)/(64)-((y-4)^2)/(80)=1}`

To find the foci, first find c where c² = a² + b²:

`\implies c=√(a^2+b^2)`

`\implies c=√(64+80)`

`\implies c=√(144)`

`\implies c=12`

Substitute the found value of c, along with the values of h and k into the foci formula:

`\implies (h+c, k)=(1+12, 4)=(13,4)`

`\implies (h-c,k)=(1-12,4)=(-11,4)`

Therefore, the foci are (-11, 4) and (13, 4).

Answer 2

• equation: (x -1)²/64 -(y -4)²/80 = 1
• foci: (-11, 4), (13, 4)

Explanation:

You want the steps to finding the equation of the hyperbola with center (1, 4), vertices (-7, 4) and (9, 4) and that includes the point (-11, -6).

Equation of a hyperbola

The standard-form equation of a hyperbola with center (h, k) and semi-axes 'a' and 'b' is ...

`((x-h)^2)/(a^2)+((y-k)^2)/(b^2)=1`

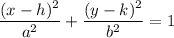
The "linear eccentricity" 'c' is the distance from the center to a focus, and satisfies the equation ...

c² = a² +b²

The vertices are (h±a, k) and the foci are (h±c, k).

Application

The center of the hyperbola is given as (1, 4). The distance from the right vertex to the center is ...

a = 9-1 = 8

The equation thus far is ...

(x -1)/8² -(y -4)/b² = 1

The value of 'b' can be determined from the given point:

(-11 -1)²/8² -(-6 -4)²/b² = 1

9/4 -100/b² = 1

5/4 = 100/b²

b² = 100/(5/4) = 80

The linear eccentricity is ...

c² = a² +b²

c² = 64 +80 = 144

c = √144 = 12

The foci are (1±12, 4) = (-11, 4) and (13, 4).

The equation is ...

(x -1)²/64 -(y -4)²/80 = 1

Step summary

1. The given information was used to find semi-major axis 'a'.
2. Together with the given center value (h, k), and the given point, the equation was written and solved for b².
3. The value of 'c' was found from a² and b², and used to find the locations of the foci.