Question

A 100gm GOLF BALL MOVING WITH A VELOCITY OF 20m/s COLLIDES WITH A 8kg STEEL BALL AT REST. IF THE COLLISION IS ELASTIC, COMPUTE THE VELOCITIES BOTH THE BALLS AFTER COLLISION

Answer 1

Golf ball (
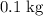`0.1\; {\rm kg}`): approximately
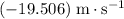`(-19.506)\; {\rm m\cdot s^(-1)}` (backwards).

Steel ball (
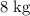`8\; {\rm kg}`): approximately
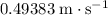`0.49383\; {\rm m\cdot s^(-1)}` (forward.)

Step-by-step explanation:

Apply unit conversion and ensure that the unit of all mass are in kilograms:
`100\; {\rm g} = 0.1\; {\rm kg}`.

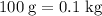In an elastic collision, both momentum
`p = m\, v` and kinetic energy
`\text{KE} = (1/2)\, m\, v^(2)` are conserved. Momentum of the two balls before the collision are:

• 
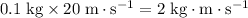  `0.1\; {\rm kg} * 20\; {\rm m\cdot s^(-1)} = 2\; {\rm kg \cdot m \cdot s^(-1)}` for the golf ball, and
• 
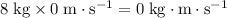  `8\; {\rm kg} * 0\; {\rm m\cdot s^(-1)} = 0\; {\rm kg \cdot m\cdot s^(-1)}` for the steel ball initially at rest.

Hence, the total momentum of the two balls was
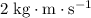`2\; {\rm kg \cdot m\cdot s^(-1)}` before the collision and (by conservation) will still be
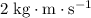`2\; {\rm kg \cdot m\cdot s^(-1)}\!` after the collision.

Kinetic energy of the two balls before the collision are:

• 
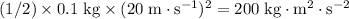  `(1/2)* 0.1\; {\rm kg} * (20\; {\rm m\cdot s^(-1)})^(2) = 200\; {\rm kg \cdot m^(2) \cdot s^(-2)}` for the golf ball, and
• 
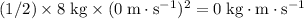  `(1/2) * 8\; {\rm kg} * (0\; {\rm m\cdot s^(-1)})^(2) = 0\; {\rm kg \cdot m\cdot s^(-1)}` for the steel ball initially at rest.

Thus, the total kinetic energy of the two balls will be
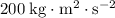`200\; {\rm kg \cdot m^(2) \cdot s^(-2)}` before and after the collision.

Let
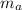`m_(a)` and
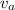`v_(a)` denote the mass and velocity of the golf ball after collision;
`m_(a) = 0.1\; {\rm kg}`.

Let
`m_(b)` and
`v_(b)` denote the mass and velocity of the steel ball after collision;
`m_(b) = 8\; {\rm kg}`.

Total momentum after the collision shall be
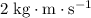`2\; {\rm kg \cdot m\cdot s^(-1)}\!`. Thus:

`m_(a)\, v_(a) + m_(b)\, v_(b) = 2\; {\rm kg \cdot m\cdot s^(-1)}`.

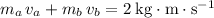Total kinetic energy after the collision shall be
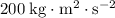`200\; {\rm kg \cdot m^(2) \cdot s^(-2)}`. Thus:

`\displaystyle (1)/(2) \, m_(a)\, v_(a) + (1)/(2)m_(b)\, v_(b) = 200\; {\rm kg \cdot m^(2)\cdot s^(-2)}`.

Assume that the unit of
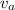`v_(a)` and
`v_(b)` are both "meters per second" (
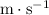`{\rm m\cdot s^(-1)}`.) Combine and solve this system of two equations and two variables:

`\left\lbrace\begin{aligned}&0.1\, v_(a) + 8\; v_(b) = 2 \\ &(1)/(2)\, {v_(a)}^(2) + 4\, {v_(b)}^(2) = 200\end{aligned}\right.`.

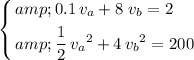Rewrite the first equation to obtain
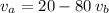`v_(a) = 20 - 80\, v_(b)`. Substitute this equation into the second one to eliminate
`v_(a)`:

`\displaystyle (1)/(2)\, (20 - 80\, v_(b))^(2) + 4\, v_(b)^(2) = 200`.

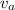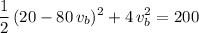Solve this equation for
`v_(b)`:

`324\, {v_(b)}^(2) - 160\, v_(b) = 0`.

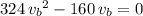There are two solutions to this quadratic equation:
`(40 / 81)` and
`0`. Note that the velocity of the steel ball must be non-zero right after the collision. Hence,
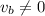`v_(b) \\e 0`. Therefore, the only possible value for
`v_(b)` will be
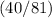`(40 / 81)\!`, which is approximately
`0.49383\; {\rm m\cdot s^(-1)}`.

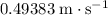Substitute
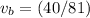`v_(b) = (40 / 81)` back into the first equation of the system and solve for
`v_(a)`:
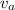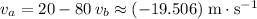`v_(a) = 20 - 80\, v_(b) \approx (-19.506)\; {\rm m\cdot s^(-1)}`. Note that the velocity of the golf ball
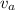`v_(a)\!` is negative since the golf ball is travelling backwards, opposite to its initial direction of motion.

In other words, the velocity right after collision will be approximately
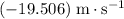`(-19.506)\; {\rm m\cdot s^(-1)}` (backwards) for the golf ball and approximately
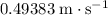`0.49383\; {\rm m\cdot s^(-1)}` (forwards) for the steel ball.