Question

Savannah is flying a kite, holding her hands a distance of 2.5 feet above the ground

and letting all the kite's string play out. She measures the angle of elevation from her
hand to the kite to be 32. If the string from the kite to her hand is 75 feet long, how
many feet is the kite above the ground? Round your answer to the nearest tenth of a
foot if necessary.
Answer:
feet Submit Prowes
Z

Answer 1

42.2 ft

Explanation:

The given scenario can be modelled as a right triangle (see attached diagram), where the angle of elevation is 32°, and the length of the kite string (75 ft) is the hypotenuse.

We want to find the distance the kite is above the ground, so we want to find the side of the right triangle that is opposite the given angle. To do this, we can use the sine trigonometric ratio.

`\boxed{\begin{minipage}{9 cm}\underline{Sine trigonometric ratio} \\\\$\sf \sin(\theta)=(O)/(H)$\\\\where:\\ \phantom{ww}$\bullet$ $\theta$ is the angle. \\ \phantom{ww}$\bullet$ $\sf O$ is the side opposite the angle. \\\phantom{ww}$\bullet$ $\sf H$ is the hypotenuse (the side opposite the right angle). \\\end{minipage}}`

Substituting θ = 32° and H = 75 into the ratio, we get:

`\sin 32^(\circ)=(\sf O)/(75)`

`\textsf{O}=75\sin 32^(\circ)`

`\textsf{O}=39.7439448...\; \sf ft`

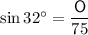
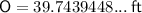
The angle of elevation is the angle between the horizontal plane and the line of sight from an observer to an object located at a higher position.

In this scenario, the angle of elevation is measured from Savannah's hand, which is a distance of 2.5 ft above the ground. Therefore, we need to add 2.5 ft to the value of O found using the sine ratio.

`\implies 39.7439448...+2.5=42.2\; \sf ft\;(nearest\;tenth)`

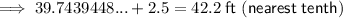
Therefore, the kite is 42.2 ft above the ground (rounded to the nearest tenth).