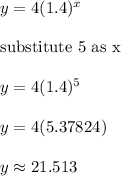Question

Tough question !!! Help

Answer 1

`y = 4(1.4)^x`

`\text{at x = 5, }y=21.513`

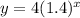
Explanation:

If you think about an exponential function in the form:
`f(x) = a(b)^x`

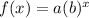
you'll realize a pattern, which is by definition.

Evaluating the function at x = 1:
`f(1) = a(b)^1 \implies a(b)`

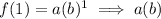
Evaluating the function at x = 2:
`f(2) = a(b)^2 \implies a(b * b)`

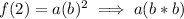
Evaluating the function at x = 3:
`f(3) = a(b)^3\implies a(b * b * b)`

Each term just has an additional "b" that it's being multiplied by. This is by definition of an exponential function, repeated multiplication.

You'll also notice something else interesting, we can find this "b" value by dividing any term by it's previous term.

Take for example f(1) and f(2):
`(a(b* b))/(a(b))\to b`

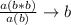
As mentioned before, as x increases by one, we just have another term to multiply by. So if we divide by the previous term (where x is one less), then we should just have this "b" value, which is the generally expressed in either a growth or decay rate.

So now that we know that, we can divide f(2) by f(1) using the values shown on the graph:

given:

`f(1) = 5.6\\f(2) = 7.84`

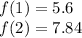
Let's divide the f(2) by f(1) to get:
`(7.84)/(5.6) \to1.4`

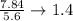
Lastly to find our "a" value, we just need to find the y-intercept, since when x = 0, the b will be equal to one (since anything raised to the power of zero is one), we can just look at the graph to see the y-intercept.

Looking at the graph, we can see the y-intercept is four, so a = 4.

Another way to do this algebraically rather than visually, would be to use our knowledge of exponentials to realize that as x increases by one (when we're going right), the y-value is just being multiplied by "b" as mentioned before.

So as x decreases by one (when we're going left) the y-value is just being divided by "b".

So f(0) should be equal to f(1) / b, and we know both values! Which are going to substitute into:
`(5.6)/(1.4)\to 4`

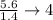
Anyways, once we plug in "a" and "b" into the standard form of an exponential function, we get:
`y = 4(1.4)^x`

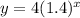
We can now use this equation to find y-values that are not shown in the graph.

To find the x-value at x = 5, simply substitute in "5" as x

`y = 4(1.4)^x\\\\\text{substitute 5 as x}\\\\y=4(1.4)^5\\\\y=4(5.37824)\\\\y\approx 21.513`