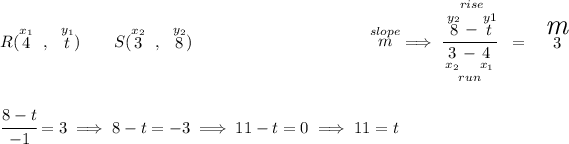well, we know that R, S and T are on the same straight line, hmmmm wait a second!! that means that the slope for RS must be the same as the slope for ST, heck, what's the slope for ST anyway?
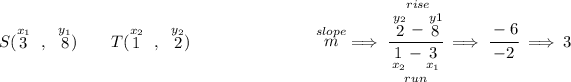
ahha!! that means that the slope for RS is really 3, hmmmm