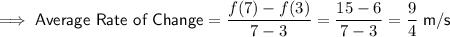Answer:
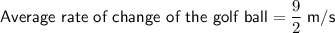
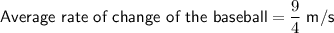
Explanation:
The average rate of change of function f(x) over the interval a ≤ x ≤ b is given by:
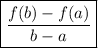
To find the average rate of change from 3 to 7 seconds:
Therefore, use the formula:
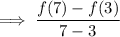
Golf Ball

From inspection of the table:
Substitute these values into the formula to find the average rate of change of the golf ball from 3 seconds to 7 seconds:

Baseball
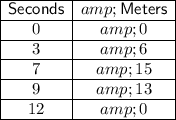
From inspection of the table:
Substitute these values into the formula to find the average rate of change of the baseball from 3 seconds to 7 seconds: