Answer:
All real numbers.
Explanation:
The bars either side of an expression or a value are the absolute value symbol. "Absolute value" means how far a value is from zero. Therefore, the absolute value of a number is its positive numerical value.
Given inequality:
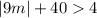
Subtract 40 from both sides to isolate the absolute value on one side of the equation:
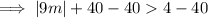
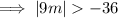
As the absolute value of a number or expression is its positive numerical value:
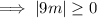
Therefore, as 9m is always greater than or equal to zero, it will always be greater than -36, regardless of the value of m.
Therefore, the solution of the given inequality is all real numbers.