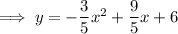Answer:

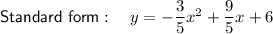
Explanation:

If the x-intercepts are (-2, 0) and (5, 0) then:
Substitute the values of p and q into the formula:
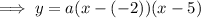
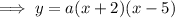
To find a, substitute the given point on the curve P (3, 6) into the equation:
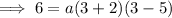
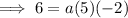
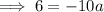
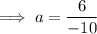
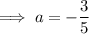
Substitute the found value of a into the equation:
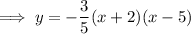
Expand to write the equation in standard form: