Question

The American bullfrog (Rana catesbeiana) can jump a distance of

nearly 15 times its length! If a bullfrog starts on a horizontal log and
leaps with a velocity of 4.40 m/s at an angle of 37.0° to the horizontal,
what distance can it cover?

Answer 1

Approximately
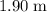`1.90\; {\rm m}` (assuming that
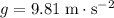`g = 9.81\; {\rm m\cdot s^(-2)}` and that air resistance on the bullfrog is negligible.)

Step-by-step explanation:

It is given that the initial velocity
`u` is at an angle of
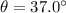`\theta = 37.0^(\circ)}` above the horizontal. Therefore:

• Initial vertical velocity:
  `u_(y) = u\, \sin(\theta) \approx 2.64799\; {\rm m \cdot s^(-1)}`.
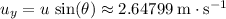• Initial horizontal velocity:
  `u_(x) = u\, \cos(\theta) \approx 3.51400\; {\rm m \cdot s^(-1)}`.

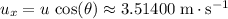If air resistance on the bullfrog is negligible, final vertical velocity right before landing will be the opposite of the initial vertical velocity:

`v_(y) = (-u_(y)) = (-2.64799)\; {\rm m\cdot s^(-1)}`.

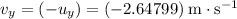Change in vertical velocity:

`(v_(y) - u_(y)) = (-2.64799) \; {\rm m\cdot s^(-1)} - 2.64799 \; {\rm m\cdot s^(-1)} \approx (-5.29598)\; {\rm m\cdot s^(-1)}`.

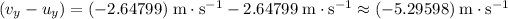Vertical acceleration of the bullfrog will be
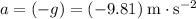`a = (-g) = (-9.81)\; {\rm m\cdot s^(-2)}` while the frog is in the air. Therefore, time required for the velocity to change will be:

`\begin{aligned} t &= (v_(y) - u_(y))/(a_(y)) \\ &= (v_(y) - u_(y))/((-g)) \\ &\approx \frac{(-5.29598)\; {\rm m\cdot s^(-1)}}{(-9.81)\; {\rm m\cdot s^(-2)}} \\ &\approx 0.53985\; {\rm s}\end{aligned}`.

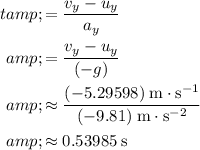If air resistance on the bullfrog is negligible, horizontal velocity will be constant:
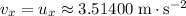`v_(x) = u_(x) \approx 3.51400\; {\rm m\cdot s^(-2)}`. After
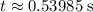`t \approx 0.53985\; {\rm s}` in the air, the horizontal displacement of the bullfrog will be:

`\begin{aligned}x_(x) &= v_(x)\, t \\ &\approx 3.51400\; {\rm m\cdot s^(-1)} * 0.53985\; {\rm s} \\ &\approx 1.90\; {\rm m} \end{aligned}`.

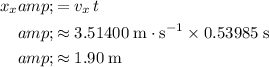Therefore, this bullfrog will cover a distance of approximately
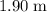`1.90\; {\rm m}`.