Answer:
Part A
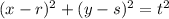
where:
- (r, s) is the center of the circle.
- (x, y) is a point on the circle.
- t is the radius of the circle.
Part B
Domain = [-3, 17]
Range = [-14, 6]
Part C
Point (9, 1) is inside the border of the circle.
Explanation:
Part A

From inspection of the given triangle:
Substitute these values into the formula to derive the standard equation of the circle:
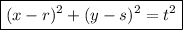
where:
- (r, s) is the center of the circle.
- (x, y) is a point on the circle.
- t is the radius of the circle.
Part B
Given the center of the circle (r, s) is (7, -4) and the radius (t) is 10.
The domain of the circle is the x-value of the center minus and plus the radius:
![\begin{aligned}\implies \textsf{Domain}&=[r-t,r+t]\\&= [7-10, 7+10] \\&= [-3, 17]\end{aligned}](https://img.qammunity.org/2023/formulas/mathematics/college/4fuzayvhbl0lniu9ku9pai8z7nquehrd72.png)
The range of the circle is the y-value of the center minus and plus the radius:
![\begin{aligned}\implies \textsf{Range}&=[s-t,s+t]\\&=[-4-10, -4+10]\\& = [-14, 6]\end{aligned}](https://img.qammunity.org/2023/formulas/mathematics/college/97ld43dz3ry92ojlpsvtwuq47i5z6nimt6.png)
Part C
Substitute (r, s) = (7, –4) and t = 10 into the derived equation from part A:
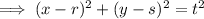
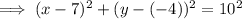
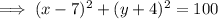
Substitute the given point (9, 1) into the equation:

As 29 < 100, the point (9, 1) is inside the border of the circle.