Answer: y = 2x - 9
=========================================================
Step-by-step explanation:
Let's find the slope of the line through the given points.
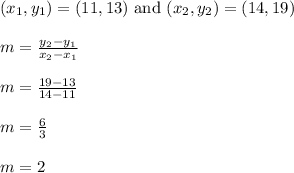
The slope is 2.
Now apply point-slope form and solve for y as shown in the steps below.
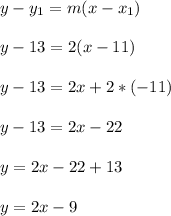
The answer is y = 2x - 9
It's of the form y = mx+b
- m = 2 = slope
- b = -9 = y intercept
----------------------------------------
Check:
Let's plug in x = 11.
We should get y = 13 as a result because of the point (11,13)
So,
y = 2x-9
y = 2*11-9
y = 22 - 9
y = 13
This confirms y = 2x-9 goes through (11,13)
Follow similar steps to show that x = 14 leads to y = 19.
I'll let you do this part.