Answer:
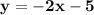
Explanation:
The equation of a line in slope-intercept form is represented by
y = mx + c
where
m is the slope
c is the y-intercept
First of all we have to find the slope from the two points given by using the formula
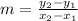
where
(x1, y1) and (x2, y2) are the points
From the question the points are (-3,1) and (4, -13)
We have
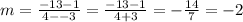
Next we find the y-intercept 'c' by placing one of the points and the slope into the slope-intercept form equation
Using point (-3,1) and m = -2
We have

Since we have both m and c we can place it into the main equation to find the equation
Using point and m = -2 c= -5
We have the final answer as
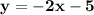
Hope this helps you