Answer:
The gas is decreasing at a rate of 50 cubic centimeters per minute.
Step-by-step explanation:
The Boyle's Law is represented by the following expression:
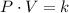 (1)
(1)
Where:
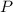 - Pressure, in kilopascals.
- Pressure, in kilopascals.
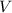 - Volume, in cubic centimeters.
- Volume, in cubic centimeters.
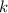 - Proportionality constant, in kilopascal-cubic centimeters.
- Proportionality constant, in kilopascal-cubic centimeters.
By definitions of rate of change and implicit differentiation, we derive the following differential equation:
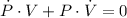 (2)
(2)
Where:
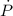 - Rate of change of the pressure, in kilopascals per minute.
- Rate of change of the pressure, in kilopascals per minute.
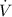 - Rate of change of the volume, in cubic centimeters per minute.
- Rate of change of the volume, in cubic centimeters per minute.
Then, we clear the rate of change of the volume within (2):
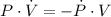
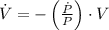
If we know that
 ,
,
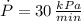 and
and
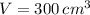 , then the rate of change of the volume is:
, then the rate of change of the volume is:
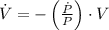
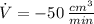
The gas is decreasing at a rate of 50 cubic centimeters per minute.