Question

Boyle's Law states that when a sample of gas is compressed at a constant temperature, the pressure P and volume V satisfy the equation PV = C, where C is a constant. Suppose that at a certain instant the volume is 300 cm3, the pressure is 180 kPa, and the pressure is increasing at a rate of 30 kPa/min. At what rate is the volume decreasing at this instant?

Answer 1

The gas is decreasing at a rate of 50 cubic centimeters per minute.

Step-by-step explanation:

The Boyle's Law is represented by the following expression:

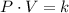`P\cdot V = k` (1)

Where:

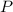`P` - Pressure, in kilopascals.

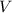`V` - Volume, in cubic centimeters.

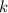`k` - Proportionality constant, in kilopascal-cubic centimeters.

By definitions of rate of change and implicit differentiation, we derive the following differential equation:

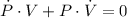`\dot P \cdot V + P\cdot \dot V = 0` (2)

Where:

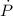`\dot P` - Rate of change of the pressure, in kilopascals per minute.

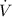`\dot V` - Rate of change of the volume, in cubic centimeters per minute.

Then, we clear the rate of change of the volume within (2):

`P\cdot \dot V = -\dot P\cdot V`

`\dot V = -\left((\dot P)/(P) \right) \cdot V`

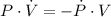
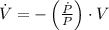
If we know that
`P = 180\,kPa`,
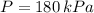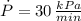`\dot P = 30\,(kPa)/(min)` and
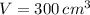`V = 300\,cm^(3)`, then the rate of change of the volume is:

`\dot V = -\left((\dot P)/(P) \right) \cdot V`

`\dot V = -50\,(cm^(3))/(min)`

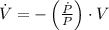
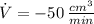
The gas is decreasing at a rate of 50 cubic centimeters per minute.