Question

1.The equation the quantity of x plus 16 all over 3 = 3x represents when two tutoring services with different rate plans charge the same fees for a session of x hours. Solve for x.

x = −7
x = −13
x = 8
x = 2
Solve the following equation for x to find the total number of people who became members of a social networking site for a certain month:

x = 0.8x + 72

2.How many people became members of the site that month?

112
288
360
432
Solve for x.

3.one fifth times the absolute value of the quantity x minus 4 end quantity minus 3 equals 6

x = −49 and x = 41
x = −41 and x = 49
x = −19 and x = 11
x = −11 and x = 19
4.Solve for x: −2(x + 3) = −2x − 6

0
3
All real numbers
No solution
5.Solve for x: three halves plus one half times x equals two x

x equals two thirds
x = 1
x = 2
x = 3

Answer 1

1. x = 2

2. x = 360

3. x = -41 and x = 49

4. All real numbers.

5. x = 1

Explanation:

Question 1

`\begin{aligned}&\textsf{Given}: & (x+16)/(3)&=3x\\&\textsf{Multiply both sides by 3}: & x+16&=9x\\&\textsf{Subtract $x$ from both sides}: & 16&=8x\\&\textsf{Divide both sides by 8}: & x&=2\end{aligned}`

Therefore, the solution is x = 2.

Question 2

`\begin{aligned}&\textsf{Given}: & x &= 0.8x + 72\\&\textsf{Subtract $0.8x$ from both sides}: & 0.2x&=72\\&\textsf{Divide both sides by 0.2}: & x&=360\end{aligned}`

Therefore, the solution is x = 360.

Question 3

`\begin{aligned}&\textsf{Given}: & (1)/(5)|x-4|-3&=6\\&\textsf{Add 3 to both sides}: & (1)/(5)|x-4|&=9\\&\textsf{Multiply both sides by 5}: &|x-4|&=45 \\\end{aligned}`

Set the contents of the absolute value equal to both the positive and negative value of the number on the other side of the equation, and solve both equations.

`\begin{aligned}\underline{\sf Equation\; 1}&&\underline{\sf Equation\; 2}\\x-4&=45 & x-4&=-45\\x-4+4&=45+4 & \quad \quad \quad x-4+4&=-45+4\\x&=49 & x&=-41\\\end{aligned}`

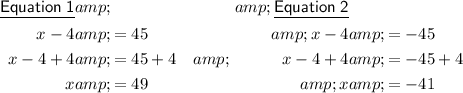
Therefore, the solutions are x = -41 and x = 49.

Question 4

`\begin{aligned}&\textsf{Given}: & -2(x + 3) &= -2x-6\\&\textsf{Distribute}: &-2x-6&=-2x-6\\&\textsf{Add 6 to both sides}: & -2x&=-2x\\&\textsf{Divide both sides by -2}: & x&=x\end{aligned}`

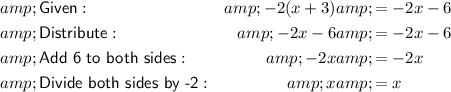
Therefore, the solution is all real numbers.

Question 5

`\begin{aligned}&\textsf{Given}: & (3)/(2)+(1)/(2)x & = 2x\\&\textsf{Subtract $(1)/(2)x$ from both sides}: & (3)/(2)&=(3)/(2)x\\&\textsf{Multiply both sides by 2}: & 3&=3x\\&\textsf{Divide both sides by 3}: & 1&=x\end{aligned}`

Therefore, the solution is x = 1.