Answer:
t(r) = log(r)/log(5) = log₅(r)
Explanation:
You want the inverse of r(t)=5^t.
Solve for t
An exponential function is solved using logarithms.

The change of base formula can be used to simplify this a bit.
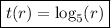
__
Additional comment
The latter form of the inverse function can be found directly at the first step by taking logarithms base 5.
The notation here is slightly different from the usual "inverse function" notation, where we designate the inverse of f(x) using f⁻¹(x). The notation we have used recognizes that the function r(t) generates ordered pairs (t, r), and the inverse function t(r) generates ordered pairs (r, t).
You are welcome to make use of whatever inverse function notation will satisfy your grader.