Question

A square, two congruent trapezoids, and two congruent semicircles were used to form the figure shown. Which measurement is closest to the area of the figure in square centimeters? 40 cm 37cm² 28 cm² 55 cm²​

Answer 1

B. 37 cm²

Explanation:

`\boxed{\begin{minipage}{4.5 cm}\underline{Area of a square}\\\\$A=s^2$\\\\where $s$ is the side length.\\\end{minipage}}`

Given the side length of the square is 4 cm:

`\begin{aligned}\implies \sf Area\;of\;the\;square&=4^2\\&=\sf 16\;cm^2\end{aligned}`

`\boxed{\begin{minipage}{4.5 cm}\underline{Area of a semicircle}\\\\$A=(1)/(2)\pi r^2$\\\\where $r$ is the radius. \\\end{minipage}}`

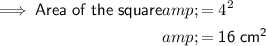
The radius of a circle is half its diameter.

Given the diameter of the semicircles is 2 cm, then their radius is 1 cm.

`\begin{aligned}\implies \textsf{Area of one semicircle}&= \sf (1)/(2) \pi (1)^2\\& = \sf (1)/(2) \pi \; cm^2\end{aligned}`

`\boxed{\begin{minipage}{4.5 cm}\underline{Area of a trapezoid}\\\\$A=(1)/(2)(a+b)h$\\\\where:\\ \phantom{ww}$\bullet$ $a$ and $b$ are the bases. \\ \phantom{ww}$\bullet$ $h$ is the height.\\\end{minipage}}`

Given the bases of the trapezoids are 2 cm and 4 cm, and their height is 3 cm:

`\begin{aligned}\implies \textsf{Area of one trapezoid}&= \sf (1)/(2) (2+4)(3)\\&= \sf (1)/(2) (6)(3)\\&= \sf (3)(3)\\&=\sf 9\;cm^2\end{aligned}`

Given the figure is made up of a square, two congruent trapezoids and two congruent semicircles:

`\begin{aligned}\implies\textsf{Area of the figure}&= \sf square+2\;trapezoids+2\; semicircles\\&= \sf 16+2(9)+2\left((1)/(2) \pi\right)\\& = \sf 16 + 18 + \pi \\& = \sf 34 + \pi \\& = \sf 37.14159...\; cm^2\end{aligned}`

Therefore, the measurement that is closest to the area of the figure in square centimeters is 37 cm².