Question

A machine used to fill beverage cans is supposed to supply exactly 16 ounces toeach can, but the actualamount supplied varies randomly from can to can. The machine is calibrated so that the population standard deviation is 0.04 ounces. How many filled cans must be sampled so that we estimate the mean fill volume within 0.015 ounces with 99% confidence

Answer 1

48 cans must be sampled.

Explanation:

We have that to find our
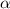`\alpha` level, that is the subtraction of 1 by the confidence interval divided by 2. So:

`\alpha = (1 - 0.99)/(2) = 0.005`

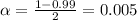
Now, we have to find z in the Ztable as such z has a pvalue of
`1 - \alpha`.

That is z with a pvalue of
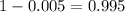`1 - 0.005 = 0.995`, so Z = 2.575.

Now, find the margin of error M as such

`M = z(\sigma)/(√(n))`

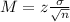
In which
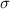`\sigma` is the standard deviation of the population and n is the size of the sample.

The machine is calibrated so that the population standard deviation is 0.04 ounces.

This means that
`\sigma = 0.04`

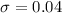
How many filled cans must be sampled so that we estimate the mean fill volume within 0.015 ounces with 99% confidence?

n cans must be sampled, and n is found when M = 0.015. So

`M = z(\sigma)/(√(n))`

`0.015 = 2.575(0.04)/(√(n))`

`0.015√(n) = 2.575*0.04`

`√(n) = (2.575*0.04)/(0.015)`

`(√(n))^2 = ((2.575*0.04)/(0.015))^2`

`n = 47.2`

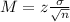
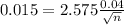
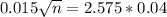
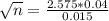
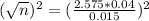
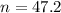
Rounding up, 48 cans must be sampled.