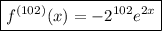It looks like you're given
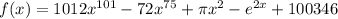
and are asked to find the 102nd derivative of f(x).
Recall the power rule: for integer n,
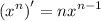
This means that the power of x reduces to 0 after differentiating n times, and you're left with a constant coefficient n! :
• after differentiating 2 times,
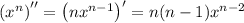
• after differentiating 3 times,
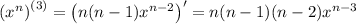
• and so on, up to the n-th time, which yields
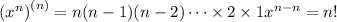
As soon as you have a constant, the next derivative will be 0. This means that after differentiating 102 times, the first 3 terms of f(x), as well as the constant term, will vanish.
Recall the chain rule:
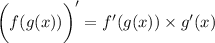
Then the first few derivatives of the exponential term are
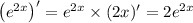
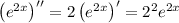
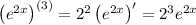
and so on, with n-th derivative
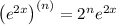
Putting everything together, we have