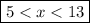1 Answer

Loktar · Answer 1 · 2023-08-11T03:46:43+0000

Answer:

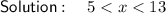
$\textsf{Solution}: \quad 5 < x < 13$

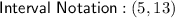
$\textsf{Interval Notation}: (5, 13)$

Explanation:

Given inequality:

|x-9|-3 < 1

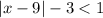
To solve an inequality containing an absolute value, isolate the absolute value on one side of the inequality:

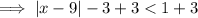
$\implies |x-9|-3 +3 < 1+3$

$\implies |x-9| < 4$

Apply the absolute rule:

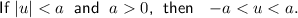
$\textsf < a$\; and\; $a > 0$, \;then \; $-a < u < a$.$

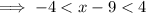
$\implies -4 < x-9 < 4$

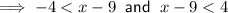
$\implies -4 < x-9 \;\; \textsf{and}\;\;x-9 < 4$

Solve case 1:

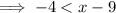
$\implies -4 < x-9$

$\implies x-9 > -4$

$\implies x-9 +9 > -4+9$

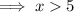
$\implies x > 5$

Solve case 2:

$\implies x-9 < 4$

$\implies x-9+9 < 4+9$

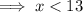
$\implies x < 13$

Therefore, x is greater than 5 and smaller than 13.

Merge the overlapping intervals to obtain the solution:

$\boxed{5 < x < 13}$

Please log in or register to add a comment.