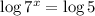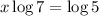Answer:

Explanation:

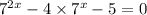
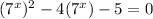
This is a quadratic equation in 7^x.
Let u = 7^x.
Substitute u for 7^x to see the quadratic equation more clearly.
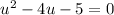
Now we have a factorable quadratic equation in u.

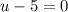 or
or

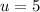 or
or

Now substitute back 7^x for u.
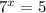 or
or
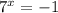
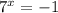 does not have a real solution.
does not have a real solution.
Continue solving
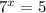 for x.
for x.
Take log of both sides.