Question

Nora leans a 24-foot ladder against a wall so that it forms an angle of 76^{\circ} ∘ with the ground. How high up the wall does the ladder reach? Round your answer to the nearest hundredth of a foot if necessary.

Answer 1

23.29 ft

Explanation:

The given scenario can be modelled as a right triangle, where the angle between the ground and the ladder is 76°, the side opposite the angle is the height the ladder reaches up the wall, and the hypotenuse is the ladder.

To find how high up the wall the ladder reaches, use the sine trigonometric ratio:

`\sin(\theta)=\sf (O)/(H)`

where:

• θ is the angle.
• O is the side opposite the angle.
• H is the hypotenuse (the side opposite the right angle).

The angle of elevation is 76°, so θ = 76°.

Let x be the height the ladder reaches up the wall, so O = x.

H is the length of the ladder, so H = 24.

Substitute the given values into the sine ratio and round the answer to the nearest hundredth:

`\sin(\theta)=\sf (O)/(H)`

`\sin(76^(\circ))= (x)/(24)`

`\sin(76^(\circ))\cdot 24= (x)/(24)\cdot 24`

`24 \sin(76^(\circ))= x`

`x=24 \sin(76^(\circ))`

`x=23.28709743...`

`x=23.29\; \sf ft\;(nearest\;hundredth)`

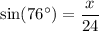
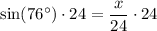
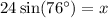
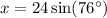
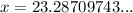
Therefore, the ladder reaches 23.29 ft up the wall, rounded to the nearest hundredth.