Answer:
Explanation:
Let y be the distance the car travels, in miles. Let t be the time traveled, in hours. The speed is 45 m/h. We know that the distance the car travels is given by the equation:
Distance = (speed)*(time)
Using the assigned variables, we can rewrite this as:
d(t) = (45 m/h)(t hours)
We want an equation that will tell us the position of the car, y, at any time, t, including t = 0, the start.
d(t) = ?
At time = 0, the starting point of the car is P. We can write:
d(0) = P
For x
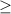 0, we would find the car at:
0, we would find the car at:
d(t) = P + (45)*t
The 45 is in units of miles/hour, t is in hours and d is in miles. Let's assume an intital position, P, for this car to be 10 miles. P = 10 miles.
The function is: d(t) = 10 + (45)*t
If we leave the units in, it can be written as: d(t) = (10 miles) + (45 miles/hr)*t(in hr)
We can see that the term "(45 miles/hr)*t(in hr)" will eventually reduce to just miles one we enter the time in hours, since the hours cancel out.
The graph of this function is attached. The line crosses the y axis at 10 (miles) when time, t, is 0 : the car has not started.
The slope of the graph can be determined by calculating the Rise/Run of the line. Pick any two points. I'll choose: (2,100) and (4,190).
Rise (change in y) is (190-100) = 90
Run (change in x) is (4 - 2) = 2
Slope = Rise/Run = (90/2) or 45.
The slope has the same value as the speed, as it should. The slope is telling us the rate of change, which for this graph, is the speed of the car. The y-intersect is (0, 10). The car is at 10 miles at the start (t=0).
To create a scenario where could have a negative value requires some imagination. There is really no such thing as negative time, except in time travel movies. But we can define t, perhaps, as the start of a race. (High noon, for example). If the cars were allowed to start moving before noon as long as they started back (negative direction) from the starting point of the race. If t is defined as "hours after 12:00 noon" then a value of t = -1 means 11:00 AM. If the car were approaching the staring line at 45 miles/hour, ahread of the official start time, the graph would make sense. Not the race, so much, but the graph would be accurate.