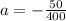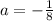Question

A) Write the vertex form by substituting in values for x, y, h, and k, and then solve for a. Show your work. (10 points)

Answer 1

y = a(x - h)^2 + k

h = 24, k = 50, x = 4, y = 0

0 = a(4 - 24)^2 + 50

0 = a(-20)^2 + 50

0 = a(400) + 50

0 = 400a + 50

400a = -50

a = - 50/400

a = - 1/8

Explanation:

that's what i put copy and paste

Answer 2

`a=-(1)/(8)`

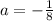
Explanation:

Given

See attachment for graph

Required

Write the vertex form and then solve for

The general equation is:

`y = a(x - h)^2 + k`

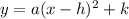
From the attachment, the vertex is at:

`(h,k) = (24,50)`

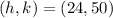
i.e.

`h = 24; k= 50`

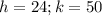
Considering point:

`(x,y) = (4,0)`

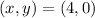
i.e.

`x=4;y=0`

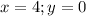
Substitute these values in
`y = a(x - h)^2 + k`

`0 = a(4 - 24)^2 + 50`

`0 = a(- 20)^2 + 50`

`0 =a(400) + 50`

`0 = 400a + 50`

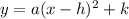
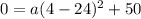
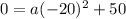
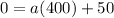
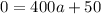
Solve for a

`400a = -50`

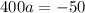
Make a the subject

`a=-(50)/(400)`

`a=-(1)/(8)`