1 Answer

Vershov · Answer 1 · 2023-09-26T19:32:15+0000

Answer:

(0, 6)

Explanation:

Given function:

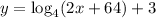
$y=\log_4(2x+64)+3$

The y-intercept of a function is the point at which the curve crosses the y-axis, so when x = 0.

Therefore, to find the y-intercept, substitute x = 0 into the function:

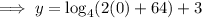
$\implies y=\log_4(2(0)+64)+3$

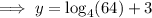
$\implies y=\log_4(64)+3$

Rewrite 64 as 4³:

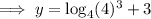
$\implies y=\log_4(4)^3+3$

$\textsf{Apply the log power law}: \quad \log_ax^n=n\log_ax$

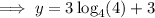
$\implies y=3\log_4(4)+3$

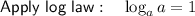
$\textsf{Apply log law}: \quad \log_aa=1$

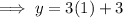
$\implies y=3(1)+3$

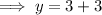
$\implies y=3+3$

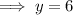
$\implies y=6$

Therefore, the y-intercept of the given function is (0, 6).

Please log in or register to add a comment.