Answer:
y=-2x-2
Explanation:
If the endpoints of the line segment are (7,4) and (-9,-4), that means that the slope will be:
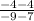 =
=
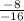 =
=
 . For the perpendicular bisector to be perpendicular to the line, it must have a perpendicular slope, which will be the negative reciprocal of
. For the perpendicular bisector to be perpendicular to the line, it must have a perpendicular slope, which will be the negative reciprocal of
 , which is -
, which is -
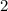 . The perpendicular bisector must also go through the midpoint of the segment, which is (-1, 0) because -1 is the average of 7 and -9 and 0 is the average of 4 and -4.
. The perpendicular bisector must also go through the midpoint of the segment, which is (-1, 0) because -1 is the average of 7 and -9 and 0 is the average of 4 and -4.
Now we find the equation!
y=mx+b. Plug in -
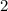 as the "m", or slope:
as the "m", or slope:
y=-
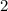 x+b
x+b
Now, plug in the point (-1, 0):
0=-
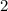 *-1+b
*-1+b
0=
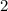 +b
+b
b=-
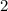
So, we have m=-
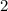 and b=-
and b=-
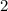 and we can form our equation!
and we can form our equation!
y=-
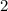 x-
x-
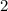
Hope this helps!! :D