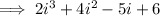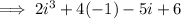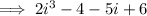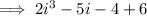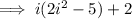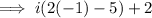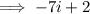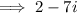Question

Use either long division or synthetic division to solve:

(2i^4 +-6i³+-25i² +31i+-30)/(i +-5)

Answer 1

`\textsf{Quotient}: \quad 2i^3+4i^2-5i+6`

`\textsf{Simplified Quotient}: \quad 2-7i`

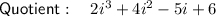
Explanation:

Long division method

• Divide the first term of the dividend by the first term of the divisor, and put that in the answer.
• Multiply the divisor by that answer, put that below the dividend.
• Subtract to create a new dividend.
• Repeat.

Given rational expression:

`(2i^4-6i^3-25i^2 +31i-30)/(i -5)`

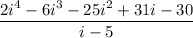
Solve using long division:

`\large \begin{array}{r}2i^3+4i^2-5i+6\phantom{)}\\i-5{\overline{\smash{\big)}\,2i^4-6i^3-25i^2 +31i-30\phantom{)}}}\\{-~\phantom{(}\underline{(2i^4-10i^3)\phantom{-b00000000000.)}}\\4i^3-25i^2+31i-30\phantom{)}\\-~\phantom{()}\underline{(4i^3-20i^2)\phantom{))))))))))))}}\\-5i^2+31i-30\phantom{)}\\-~\phantom{()}\underline{(-5i^2+25i)\phantom{........}}\\6i-30\phantom{)}\\-~\phantom{()}\underline{(6i-30)\phantom{}}\\0\phantom{)}\end{array}`

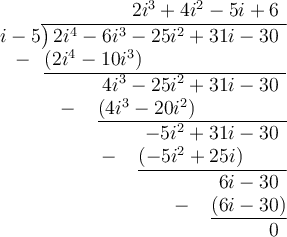
Therefore, the quotient is:

`2i^3+4i^2-5i+6`

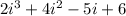
Imaginary number rule

`i^2=-1`

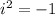
Simplify the quotient:

`\implies 2i^3+4i^2-5i+6`

`\implies 2i^3+4(-1)-5i+6`

`\implies 2i^3-4-5i+6`

`\implies 2i^3-5i-4+6`

`\implies i(2i^2-5)+2`

`\implies i(2(-1)-5)+2`

`\implies-7i+2`

`\implies 2-7i`