Question

asked Dec 14, 2023 119 views

1 Answer

FWDekker · Answer 1 · 2023-12-20T16:41:04+0000

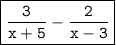
$\boxed{ \tt (3)/(x + 5) - (2)/(x - 3)}$

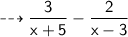
$\dashrightarrow\sf(3)/(x + 5) - (2)/(x - 3)$

Write the equation

$\\ \\$

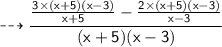
$\dashrightarrow\sf((3 * (x + 5)(x - 3))/(x + 5) - (2 * (x + 5)(x - 3))/(x - 3))/((x + 5)(x - 3))$

Take the lcm of the equation I.e (x + 5) (x + 3)

$\\ \\$

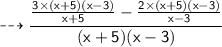
$\dashrightarrow\sf\frac{\frac{3 * \cancel{(x + 5)}(x - 3)}{\cancel{x + 5}} - \frac{2 * (x + 5)\cancel{(x - 3)}}{\cancel{x - 3}}}{(x + 5)(x - 3)}$

cancel like terms I.e (x + 5) with (x+ 5) and (x - 3) with (x - 3)

$\\ \\$

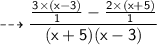
$\dashrightarrow\sf((3 * (x - 3))/(1) - (2 * (x + 5))/(1))/((x + 5)(x - 3))$

$\\ \\$

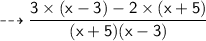
$\dashrightarrow\sf(3 * (x - 3)- 2 * (x + 5))/((x + 5)(x - 3))$

Remove 1 as denominator

$\\ \\$

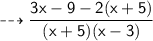
$\dashrightarrow\sf(3x - 9- 2 (x + 5))/((x + 5)(x - 3))$

Multiply 3 with x - 9

$\\ \\$

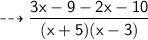
$\dashrightarrow\sf(3x - 9- 2 x - 10)/((x + 5)(x - 3))$

Multiply - 2 with x + 5

$\\ \\$

$\dashrightarrow\sf(3x - 2x- 9 - 10)/((x + 5)(x - 3))$

Arrange the equation so that it would be easier to solve.

$\\ \\$

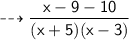
$\dashrightarrow\sf(x- 9 - 10)/((x + 5)(x - 3))$

Subtract 3x with 2x

$\\ \\$

$\dashrightarrow\bf(x-19)/((x + 5)(x - 3))$

Add -9 with - 10

$\\ \\$

$\therefore \underline {\textsf{\textbf{Option \red{one} is correct}}}$

Please log in or register to add a comment.