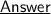
The function shown in the graph above is a discontinuous function, at x = -2
For values of x less than -2, the left side of the graph is applicable. whose equation is :
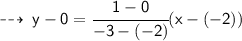
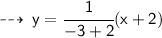
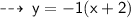

For values of x greater than -2, the right side of the graph is applicable. whose equation is :
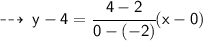
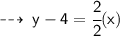
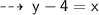
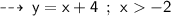
So, the correct choice will be Option " A "