Explanation:
at first multiply the factors

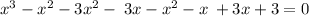
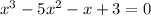
Here we see the highest power is 3 so the degree of the equation is 3
As for the real roots, the factors each as in (x-1), (x-3) & (x+1) can be considered zero each to find the real roots because for the value of x to be zero any of the multiplied factors must be zero.
either, x-1=0
=> x = 1
or, x+1=0
=> x = -1
or, x-3=0
=> x = 3
real roots of x are: 1, -1 and 3