well, one focus point at (9 , 0) and another at (-9 , 0) will mean the major axis runs over the x-axis, with a center at the origin, so the "c" distance will be 9 units, and since the major axis is 36 units, that means its "a" component or namely its half is half of 36 or 18 units, so
![\textit{ellipse, horizontal major axis} \\\\ \cfrac{(x- h)^2}{ a^2}+\cfrac{(y- k)^2}{ b^2}=1 \qquad \begin{cases} center\ ( h, k)\\ vertices\ ( h\pm a, k)\\ c=\textit{distance from}\\ \qquad \textit{center to foci}\\ \qquad √( a ^2- b ^2) \end{cases} \\\\[-0.35em] ~\dotfill\\\\ \begin{cases} a=18\\ h=0\\ k=0 \end{cases}\implies \cfrac{(x- 0)^2}{ 18^2}+\cfrac{(y- 0)^2}{ b^2}=1\qquad \textit{we also know that }C=9](https://img.qammunity.org/2023/formulas/mathematics/college/xvm1cv7tm90pze07wls7755xhaullthu1y.png)
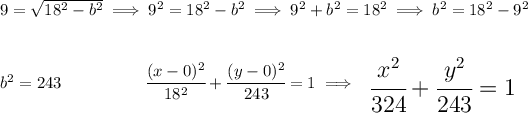
Check the picture below.