Answer:
Approximately
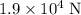 (rounded up) assuming that
(rounded up) assuming that
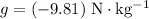 (downwards.)
(downwards.)
Step-by-step explanation:
The car is accelerating at a constant
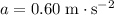 (positive since the car is accelerating upwards.) Hence, the net force on this car will be:
(positive since the car is accelerating upwards.) Hence, the net force on this car will be:
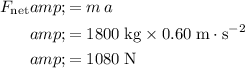 .
.
Note that since net force points in the same direction as acceleration (upwards,)
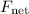 is also positive.
is also positive.
The main forces on this car are:
- Weight (downward).
- Tension from the cable (upward):
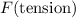 .
.
With a mass of
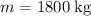 , the weight on this car will be
, the weight on this car will be
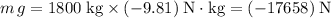 (negative since weight points downwards to the ground.)
(negative since weight points downwards to the ground.)
The net force on this car is the sum of the external forces:
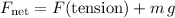 .
.
It is shown that
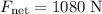 while
while
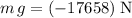 . Substitute both values into the equation and solve for
. Substitute both values into the equation and solve for
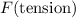 :
:
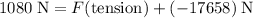 .
.
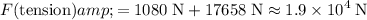 (rounded up.)
(rounded up.)