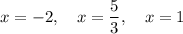Answer:
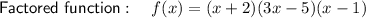
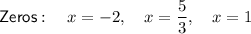
Explanation:
Given function:
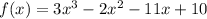
If (x + 2) is a factor then:
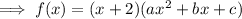
Expand:
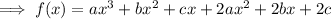
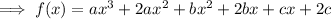
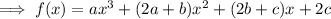
To find a, compare the coefficients of x³:
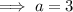
To find b, substitute the found value of a into the coefficient for x² and compare:
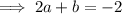
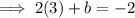
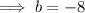
To find c, compare the constants:
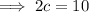

Therefore:
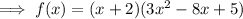
Now factor (3x²-8x+5):
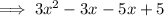
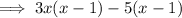
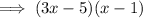
Therefore the factored function is:
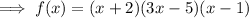
Zero Product Property
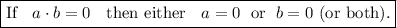
To find the zeros, set each factor equal to zero and solve for x:
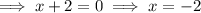


Therefore, the zeros of the function are: