Answer:
b = (4/3), with rounding
Explanation:
Area = A, in cm^2
n = days
A(n) =
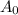

------------------
Data:
n = 2, A = 1.8
A(n) =
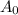

1.8 =
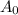
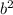
n = 3, A = 2.4
2.4 =
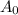
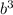
Although we are not given the initial area, we can still make the calculation since we have two data points and each has the same initial area,
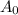 . Lets take the first equation and multiply it by b, in order to bring the
. Lets take the first equation and multiply it by b, in order to bring the
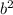 to
to
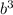
1.8 =
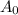
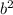
b(1.8 =
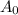
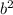 )
)
1.8b =
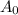
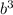
We can know from the second equation that 2.4 =
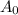
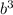 . We can eliminate this term in the above relationship by substituting 2.4:
. We can eliminate this term in the above relationship by substituting 2.4:
1.8b =
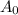
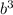
1.8b = 2.4
b = 1.3333
or (4/3)
Check:
Does the value of (4/3) for b work for both data points? To check this, we do need to assume an initial starting area. Lets assume the starting area,
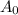 = 1.
= 1.
n = 2, A = 1.8, b = (4/3)
A(n) =
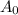

1.8 = 1*
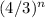
1.8 = 1.78 Close enough?
n = 3, A = 2.4, b = (4/3)
2.4 =
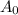
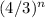
2.4 = 1*
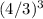
2.4 = 2.37 Close enough?