Question

Express your answer as a polynomial in standard form.

f(x)= -3x+5
g(x)=x^2+2x+15
Find: (g∘f)(x)

Answer 1

Answer:
`(g \circ f)(x)=9\text{x}^2-36\text{x}+50\\\\`

=====================================================

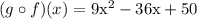
Step-by-step explanation:

The notation (g∘f)(x) is the same as g(f(x))

We'll start with the outer function g(x). Then replace each x with f(x). Afterward plug in f(x) = -3x+5 for the right hand side only.

This is what the steps look like

`g(\text{x})=\text{x}^2+2\text{x}+15\\\\g(f(\text{x}))=(f(\text{x}))^2+2f(\text{x})+15\\\\g(f(\text{x}))=(-3\text{x}+5)^2+2(-3\text{x}+5)+15\\\\g(f(\text{x}))=9\text{x}^2-30\text{x}+25-6\text{x}+10+15\\\\g(f(\text{x}))=9\text{x}^2-36\text{x}+50\\\\`

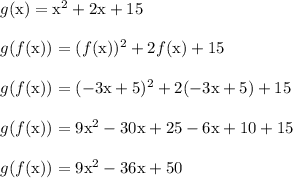
Therefore,

`(g \circ f)(x)=9\text{x}^2-36\text{x}+50\\\\`

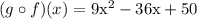
You can use tools like WolframAlpha, GeoGebra, and Desmos as ways to confirm the answer.