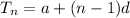Question

If the second term of an arithmetic sequence is 7 and the fourth term is 1, what is the 15th term? (non complicated answer would be extremely appreciated <3)

Answer 1

⇒
`T_(n) =a+(n-1)d` is the formula to find the general term of the arithmetic sequence.

⇒Note to find the second term we will plug in 2 in the place of n in the formular and simplify.

⇒
`T_(2) =a+(2-1)d\\T_(2) =a+(1)d\\T_(2) =a+d`

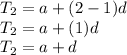
⇒It is given that the second term is 7 meaning in the place of
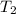`T_(2)` in the equation above since we do not know the value of a and d we will plug in 7 and have the equation
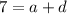`7=a+d` as our first equation.

⇒ For the fourth term
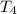`T_(4)` we follow the same step of using the general formula to find the nth term by plugging in 4 in the place of n and and simplify

`T_(4) =a+(4-1)d\\T_(4)=a+(3)d\\T_(4)=a+3d`

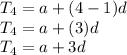
In the place of
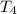`T_(4)` plug in 1 for the fourth term is equal to 1 to have the second equation

`1=a+3d`

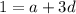
Note we can now use the two equations we have now to find the value of a which is the first term and d which is the difference.

7=a+d......1st equation

1=a+3d...2nd equation

∴from the first equation by making a the subject of the equation we get

a=7-d

from the second equation making a the subject of the equation we get a=1-3d

Now let us equate first equation and the second equation since they are both equal to a and solve for d.

`7-d=1-3d\\-d+3d=1-7\\2d=-6\\(2d)/(2) =(-6)/(2) \\d=-3`

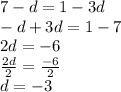
⇒Now you can see that we have the difference of the arithmetic sequence equal to -3

⇒To find the value of a you can use any of the equations from the ones we created . I will use the equation a=7-d

`d=-3\\a=7-d\\a=7-(-3)\\a=7+3\\a=10`

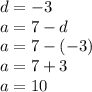
⇒ to get the 15th term we will go back to the general formula of finding the nth term in the place if n we will plug in 15 and simplify the formula

`T_(15) =a+(15-1)d\\T_(15)=a+(14)d\\T_(15)=a+14d\\`

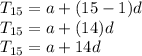
⇒Now we find that the 15th term is equal to a plus 14(d)

⇒Note we already have the value of a and we can just plug them in to find the value of the 15th term and simplify.

`a=10,d=-3\\T_(15)=a+14d\\\\T_(15)=10+14(-3)\\T_(15)=10-42\\T_(15)=-32`

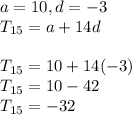
⇒The 15th term is -32