Answer:
b) The quadratic equation has two distinct real number roots.
Explanation:
Rule: If the discriminant (
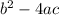 ) :
) :
is = 0, one root
is > 0, 2 real roots
is < 0, 0 real root, 2 complex roots.
-The reason is because complex numbers include imaginary numbers, which occur when you try to calculate the square root of a negative number.
Lets find the discriminant.
a: 9
b: 3
c: -2
Plug into the formula.
(3)^2 - 4(9)(-2)
Simplify.
9 + 72
81
Because the discriminant (81) is greater than 0, it has 2 real number roots.