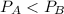Answer:
Water pressure is greatest at point B where the diameter is larger
Step-by-step explanation:
This is due to Bernoulli's Equation:
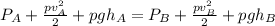
and Continuity Equation:
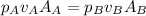
where...
P = Pressure of Fluid at the Center of the Pipe
ρ = Density of Fluid
v = Velocity of Fluid
g = Gravitational Constant
h = Height of Fluid at the Center of the Pipe
A = Area of Pipe Cross Section
This is the same as saying the following:
Pressure Energy (
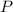 ) + Kinetic Energy (
) + Kinetic Energy (
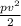 ) + Potential Energy (
) + Potential Energy (
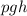 ) = Constant
) = Constant
The height of flow at the center of the pipe is the same, so we know that Potential Energy cancels out on both sides of the equation (Δ
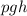 = 0)
= 0)
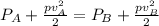
Now that we've simplified Bernoulli's Equation, we need to determine which Pressure is greater using Continuity Equation.
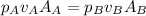
Density is the same, so we can cancel this out on both sides of the equation (Δρ = 0)
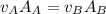
From the problem statement, we know that

Since
 , we know that
, we know that
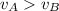 due to the Continuity Equation.
due to the Continuity Equation.
Answer: Jumping back to Bernoulli's Equation, we know that