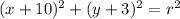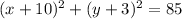Question

Write the standard equation of the circle with center (– 10, –3) that passes through the point (-3,3).

Answer 1

`(x+10)^2 + (y+3)^2 = 85`

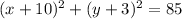
Explanation:

Equation of a circle:

The standard equation of a circle with center
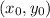`(x_0,y_0)` is given by:

`(x - x_0)^2 + (y - y_0)^2 = r^2`

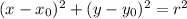
In which r is the radius.

Center (– 10, –3)

This means that
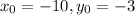`x_0 = -10, y_0 = -3`. So

`(x - x_0)^2 + (y - y_0)^2 = r^2`

`(x - (-10))^2 + (y - (-3))^2 = r^2`

`(x+10)^2 + (y+3)^2 = r^2`

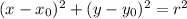
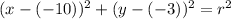
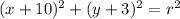
Passes through the point (-3,3).

This means that we use
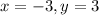`x = -3, y = 3` to find the radius squared. So

`(x+10)^2 + (y+3)^2 = r^2`

`(-3+10)^2 + (3+3)^2 = r^2`

`r^2 = 49 + 36`

`r^2 = 85`

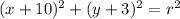
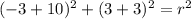
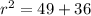
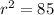
The equation of the circle is:

`(x+10)^2 + (y+3)^2 = r^2`

`(x+10)^2 + (y+3)^2 = 85`