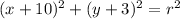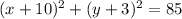Answer:
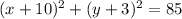
Explanation:
Equation of a circle:
The standard equation of a circle with center
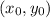 is given by:
is given by:

In which r is the radius.
Center (– 10, –3)
This means that
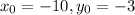 . So
. So


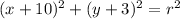
Passes through the point (-3,3).
This means that we use
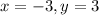 to find the radius squared. So
to find the radius squared. So
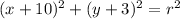
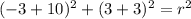

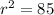
The equation of the circle is: